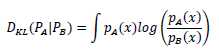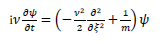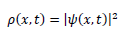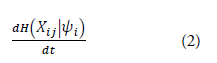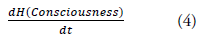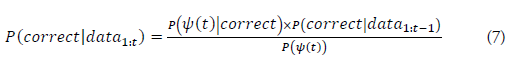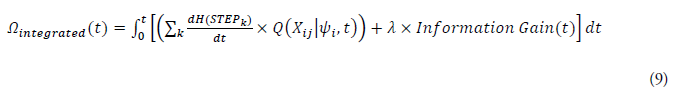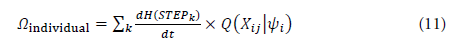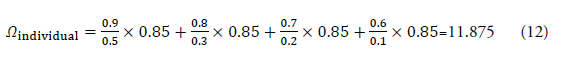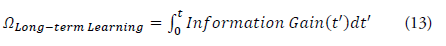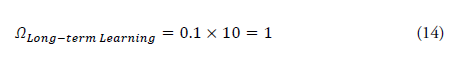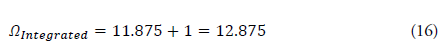Consciousness, the state of being aware of and able to think and perceive, has long been a central focus in both philosophy and neuroscience. One of the most significant advancements in this field is the development of the Integrated Information Theory (IIT), which seeks to quantify consciousness by measuring the amount of integrated information, denoted as Φ, within a system [1]. IIT posits that the greater the Φ, the higher the level of consciousness a system possesses. This theory, developed by Giulio Tononi, has significantly influenced contemporary understanding of consciousness and has led to numerous studies aiming to refine and expand on this concept [2,3].

IIT’s approach is grounded in the idea that consciousness is not merely a collection of independent components but rather a highly integrated entity where the whole is greater than the sum of its parts [4]. This integration is measured by assessing how much information a system generates when it transitions from one state to another, beyond what would be expected if the system's parts operated independently. Researchers like Tononi have argued that this measure, Φ, can explain why certain physical systems, like the human brain, are conscious, while others, such as simple machines, are not [2,4].

The idea of measuring consciousness through integrated information has inspired a variety of related metrics and theories. For instance, the Global Neuronal Workspace Theory (GNWT) and Higher-Order Thought (HOT) theories also aim to explain consciousness but from different perspectives. GNWT, proposed by Stanislas Dehaene, suggests that consciousness arises from the global availability of information across the brain [5], whereas HOT theories, like those by David Rosenthal, posit that consciousness involves a higher-order thought or awareness of one's mental states [6]. While differing in approach, these theories share with IIT the ambition to provide a quantifiable framework for understanding consciousness [5,6].

IIT is not without its critiques and alternatives. Some researchers argue that IIT’s reliance on complex mathematical formulations and its abstract nature make it difficult to test empirically [7]. For example, King and colleagues [8] highlighted the challenges in correlating IIT’s predictions with neuroimaging data. Others have proposed alternative frameworks, such as the Free Energy Principle, which suggests that consciousness and cognitive processes minimize a system's free energy, thereby maintaining its internal states within a viable range [9]. The Global Workspace Theory (GWT) developed by Baars (1988) is another prominent alternative, positing that consciousness arises from the integration of information across a globally accessible workspace in the brain. These critiques and alternatives highlight the ongoing debate and the need for further empirical validation and refinement of IIT and its related measures [7-10].

In addition to these theoretical discussions, practical applications of integrated information measures are being explored. Recent studies have compared various candidate measures of Φ across different types of neural networks, revealing significant differences in how these measures behave under different conditions [11]. For example, Tegmark [12] explored the physical substrate of consciousness, proposing a mathematical framework that aligns with IIT's principles. Such research is crucial for understanding the applicability of IIT in real-world scenarios and for refining the theory to better match empirical data [11-13]. Additionally, Mashour et al. [14] explored how integrated information could be measured in clinical settings, particularly in the context of anesthesia and consciousness recovery.

Beyond IIT, other methods for measuring consciousness have been proposed. Casali et al. [15] introduced the Perturbational Complexity Index (PCI), which measures the brain's response to a perturbation, offering a potential tool for assessing consciousness levels in patients with disorders of consciousness. Likewise, the use of entropy measures in EEG analysis has been another approach to quantifying consciousness, as explored by Baranauskas and colleagues [16]. Additionally, the Information Closure Theory suggests that conscious systems exhibit a high degree of information closure, where information is reused within the system, thereby contributing to its integration [17].

As the study of consciousness continues to evolve, it is clear that IIT and other measures of integrated information play a pivotal role in bridging the gap between philosophical concepts and scientific inquiry. This paper aims to build on these foundational ideas by proposing a new, unified measure of "consciousness strength" that integrates aspects of both real-time responsiveness and long-term learning, offering a comprehensive framework for evaluating consciousness across different systems. By drawing on existing research and refining these concepts, we hope to contribute to the ongoing development of a robust and testable theory of consciousness.

The authors have developed the HLbC (Human Language based Consciousness) model as a new framework for understanding consciousness [18]. To validate this model, they have explored its ability to explain various psychological phenomena, such as visual illusions and behavioral economics [19]. Additionally, the HLbC model has been applied to cases involving split-brain patients, where the corpus callosum has been severed, resulting in the separation of the left and right hemispheres of the brain [20]. Furthermore, discussions have been conducted on the model's compatibility with the psychological perception of time and its potential alignment with the QBism interpretation of quantum mechanics [21].

The detailed explanation is referenced in previous reports, the HLbC model is structured as follows (Figure1).

STEP-1: Observation (ψ): The system observes external events (ψ) and acquires the relevant information.

STEP-2: Matching and Selection of Options (X_ij): The observed event (ψ_i) is compared with past memories, and the system selects the most appropriate action from the available options (X_ij).

STEP-3: Action (R_j): The selected action is executed, and the outcome is obtained.

STEP-4: Memory (M): The outcome (R_j) is stored in short-term memory.

STEP-5: Post-hoc Consciousness: Based on the outcome and memory, consciousness is formed retrospectively.

In this paper, we aim to develop a metric for measuring "consciousness strength" by considering these steps.

Simulation of inverted qualia and the neural network model

First, to examine the philosophical problem of "inverted qualia"—for instance, the possibility that what one person perceives as "red" might be perceived as "blue" by another—we conducted a simulation using a neural network. The results confirmed that inverted qualia could theoretically exist within the framework of a neural network. This highlights the challenge of modeling consciousness purely based on individual qualia.

However, even if individuals experience different qualia, such as perceiving the color "red" differently, communication remains unaffected as long as they both use the same language to refer to the color as "red." This suggests that language functions as a tool for enabling shared understanding between individuals with differing qualia. Therefore, language plays a critical role in the modeling of consciousness.

The probabilistic model of language and episodic memory

Next, we define language as a probabilistic space to quantitatively address communication between observers with differing qualia. For example, if observers A and B perceive the same event F, their interpretations may differ due to the distinct probability distributions P_A and P_B that describe their observations. The Kullback-Leibler (KL) divergence is used to quantify the differences between these probability distributions, as expressed in the following equation:

When the KL divergence is zero, the probability distributions are considered equivalent, signifying that communication between the two observers is possible despite their differing qualia. This means that language can be defined as a probability space and Kullback-Leibler divergence.

Additionally, emotions are represented within the same probabilistic framework, and thus, the direct product of language and emotions also forms a probabilistic space. This allows for the creation of episodic memories, where past experiences are linked to the emotions evoked by those experiences. For instance, the memory of a "white dog running" can evoke different episodic memories depending on the emotional associations with the dog. Mathematically, these episodic memories can be modeled as probabilistic spaces, and their differences can be evaluated using the KL divergence.

Thus, episodic memories are formed as the product of language and emotions, both expressed within a probabilistic framework. This sets the stage for further detailed modeling in the following steps.

Modeling consciousness (The HLbC Model)

Finally, the HLbC model proposes that the process of consciousness arises in four key steps, as outlined below:

STEP-1: Observation of events and creation of episodes

Events observed through the senses are encoded in the brain as episodes, which are expressed as language or images. For example, the memory of observing "a white dog running" is stored in this way.

STEP-2: Association of episodes with past episodic memories

The current episode is unconsciously linked to past episodic memories, drawing on multiple previous experiences. These associations evoke emotions, creating nuanced differences in the meaning of the current episode. For example, while the episode "a white dog running" may initially seem neutral, the emotion of fear may be associated with it if the observer had a past traumatic experience with a dog.

STEP-3: Probabilistic decision-making process

The next stage involves the probabilistic selection of actions based on past episodic memories. When this decision-making process is modeled, an equation resembling the Schrödinger equation emerges. However, in this case, the variable ξ represents the Kullback-Leibler distance rather than spatial coordinates. This process is captured by the following equation:

This equation describes the stochastic nature of decision-making, and the resulting state distribution ρ(ξ,t) is given by:

Thus, decisions are made probabilistically, and the actions selected follow a distribution that can be described by this pseudo-Schrödinger equation.

STEP-4: Recognition of Actions and Emergence of Consciousness

The final step involves the brain recognizing the chosen action as a short-term memory, and this recognition is the point at which consciousness emerges. In this model, consciousness is viewed as a physical signal that is registered once an action is completed, thus providing a physicalist explanation of consciousness.

The significance of the HLbC Model

This integrated model demonstrates that language, qualia, emotions, and probabilistic decision-making all contribute to the formation of consciousness. The probabilistic decision-making process, in particular, is mathematically described using a pseudo-Schrödinger equation where the variable xxx is the Kullback-Leibler distance, not a spatial coordinate. This approach aligns with the findings of Duffy and Loch-Temzelides regarding the quantum-like properties of decision-making.

Moreover, by framing language as a probabilistic model, this work shows that even with differing qualia, individuals can communicate through a shared linguistic framework, which is a crucial step toward the development of artificial consciousness.

The HLbC model considers the creation of consciousness as an afterthought to one's unconscious actions and thus operates within a different framework from IIT. IIT measures the strength of consciousness based on integrated information. In contrast, the HLbC model previously lacked a clear metric for quantifying the strength of consciousness. The aim of this study is to propose such a metric, and the details are presented below.

Proposal of 1^st metrics

Time evolution of information entropy at each step

First, the time evolution of information entropy at each step is defined as follows:

1) STEP-1: Observation

The time evolution of the information entropy of the observed event ψ_i:

This concept is rooted in the idea that information entropy reflects the uncertainty or unpredictability of the system's state, as discussed in Shannon's foundational work on information theory [22].

2) STEP-2: Action selection

The time evolution of the information entropy during action selection:

This builds on the understanding of decision-making processes as involving the selection of actions based on probabilistic inference, which has been extensively analyzed in the context of cognitive and neural processes [9,23].

3) STEP-3,4 : Short-term memory of the action outcome

The time evolution of the information entropy of the action outcome

The retention and processing of action outcomes in short-term memory are crucial for adaptive behavior, as shown in studies on working memory and neural encoding of information [24,25].

4) STEP-5: Emergence of consciousness

The time evolution of the information entropy in the emergence of consciousness:

The emergence of consciousness has been linked to the integration of information across different neural subsystems, consistent with the principles of Integrated Information Theory [2,26].

Integration over Time

By integrating the time evolution of information entropy at each STEP, we can calculate the total change in information entropy across the entire process. This allows for an evaluation of the overall integration of information entropy over time.

For example, the total change in information entropy during STEP-1 (Observation) can be expressed as:

This approach aligns with methods used in the analysis of dynamic systems, where entropy is integrated over time to assess the system's evolution [27]. Similarly, integration is performed for the other STEPs.

Definition of consciousness strength Ω_individual :

The consciousness strength Ω_individual is defined by integrating the time evolution of information entropy across all STEPs and combining them:

This equation allows for the assessment of how the time evolution of information entropy at each STEP contributes to the overall "strength of consciousness." The integration of information across time and steps reflects the system's ability to maintain and update its internal states, which is critical for both consciousness and adaptive behavior [28,29].

Proposal of 2^nd metrics S

In the section “The Probabilistic Model of Language and Episodic Memory”, we have discussed 'consciousness strength' within the HLbC model, focusing on unconscious actions and post-hoc consciousness in response to a single observed event. This discussion has emphasized that the amount of processed information and the reaction time at each stage significantly impact the perceived strength of consciousness. However, in reality, our actions are generally directed towards achieving a specific 'correct' outcome.

From the perspective of the HLbC model, the cycle of observation → selection → unconscious action and memory → post-hoc consciousness is repeated until what is considered the optimal outcome is achieved. In subsequent cycles, the observation phase involves recognizing the 'deviation from the optimal outcome.' For instance, when addressing a crisis, the 'strength of consciousness' should not be measured merely by the amount of information or reaction time; rather, it should be determined by how swiftly the crisis is understood and the correct solution is reached.

Therefore, in processes where consciousness evolves over time toward correctness, it is essential to establish a metric that reflects the strength of consciousness in terms of its progression. To model this process, we propose incorporating Bayesian statistics, allowing us to evaluate 'consciousness strength' as the system iteratively approaches the optimal outcome through unconscious actions and post-hoc adjustments.

Setting the initial hypothesis

The system starts with an initial hypothesis:

P (correct) = PPPP (correct | prior information)

This reflects the system's prior belief before new data is observed, rooted in Bayesian principles that allow for the continuous update of beliefs as new evidence is gathered [30].

Bayesian updating based on observational data

When an observational event Ω_individual is received, the system updates the probability of correctness:

Here,

• P(Ψ(t) | correct) is the likelihood of observing event, ψ(t) given that the correct hypothesis is true.
• P (Correction | data_1:t-1) is the posterior probability based on data up to time t−1.

This updating mechanism is central to Bayesian inference, which allows for iterative refinement of predictions as more data becomes available, a concept extensively explored in probabilistic modeling and machine learning [31,32].

Definition of information gain

The information gain derived from Bayesian updating is defined as follows:

where D_KL represents the Kullback-Leibler (KL) divergence, which measures the difference between the prior and posterior distributions at time t [33]. This metric quantifies the amount of information gained with each update, providing insight into the system's learning efficiency over time.

Evaluation of Long-term learning

The evaluation of long-term learning at time t, denoted as Ω_long-term(t), is defined as the time-integrated information gain:

This integral reflects the cumulative progress of the system's learning over time, aligning with the concept of cumulative information gain used in the assessment of adaptive learning systems [34].

Detailed definition of the integrated metric

1) Integration of Real-time Evaluation and Long-term Learning

The integrated metric Ω_integrated(t) combines real-time evaluation Ω_individual(t) with long-term learning evaluation

Here, each component represents:

• The real-time evaluation term, which aggregates the information processing and response speed across different steps, weighted by the appropriateness score Q(X_i,j | Ψ_i,t) [35].
• The long-term learning term, capturing the progress towards the correct response as informed by Bayesian updating.

The parameter λ adjusts the balance between real-time responsiveness and long-term learning

Expansion of the integrated metric

To compute this integrated metric, the following form is used:

This expression enables a comprehensive evaluation of both the system's real-time response and the cumulative learning progress up to time t.

In this study, we proposed a novel metric for evaluating consciousness strength based on the HLbC (Human Language based Consciousness) model. This metric emphasizes not only the amount of information processed and the reaction time at each stage but also the entire process that leads to the optimal outcome through cycles of unconscious actions and post-hoc consciousness. Unlike the Integrated Information Theory (IIT), which focuses on the degree of information integration within a system to evaluate consciousness, the HLbC model views consciousness as an evolving process, emphasizing temporal aspects such as response times and action appropriateness.

To further illustrate the practical application of this model, we suggest evaluating consciousness strength using the analogy of an autonomous driving system. While an autonomous driving system itself does not possess consciousness, it can serve as an analogy to better understand the concept of consciousness strength as proposed by the HLbC model.

Evaluating consciousness strength in autonomous driving systems

Consider an autonomous driving system facing a specific road scenario. The system operates through the following process:

STEP-1: Observation (ψ): The system uses cameras and sensors to observe the road conditions, such as detecting an obstacle ahead.

STEP-2: Matching and Selection of Options (X_ij): The system compares the observed information with past data and selects the optimal action (e.g., avoidance, deceleration, or stopping) from multiple options.

STEP-3: Action (R_j): The system executes the selected action, such as avoiding the obstacle.

STEP-4: Memory (M): The system stores the outcome of this action in short-term memory, such as whether the avoidance was successful.

STEP-5: Post-hoc Consciousness (Consciousness): The system forms a feedback loop based on the action outcome and short-term memory, preparing for more accurate decisions in future scenarios.

Numerical example and calculation of "consciousness strength"

Let us evaluate "consciousness strength" using the following hypothetical data:

• Observation Time (T_Observation): 0.5 seconds

• Number of Options (X_ij): 3 options

• Selection Time (T_Selection): 0.3 seconds

• Action Execution Time (T_Action): 0.2 seconds

• Success Rate (S): 90%

Using these values, we can calculate consciousness strength through the following steps:

Estimation of the 1^st metrics (Real-time Evaluation)

The real-time "consciousness strength" Ω_Real-time is evaluated considering the information entropy changes and reaction times at each step.

Assuming the information entropy H(STEP_k) at each step as 0.9, 0.8, 0.7, and 0.6, and the option appropriateness score Q(X_ij | Ψ_i) as 0.85, the calculation is:

Estimation of the 2^nd metrics (Long-term Learning Evaluation)

The long-term learning evaluation Ω_Long-term Learning is considered using Bayesian updating.

Assuming an information gain of 0.1 over a 10-second period:

Integrated evaluation:

The overall "consciousness strength" Ω_Integrated is evaluated by combining real-time and long-term learning evaluations.

Assuming λ = 1:

As demonstrated in this example, utilizing an autonomous driving system as an analogy allows us to concretely evaluate "consciousness strength" based on the HLbC model. This approach does more than merely measure information processing or reaction times; it captures how a system evolves toward the optimal outcome over time. This research opens new avenues for consciousness studies, particularly in the fields of autonomous driving and artificial intelligence.

This translation maintains a scholarly tone suitable for publication in Nature, accurately reflecting the complexity and specificity of the original content while ensuring clarity and precision.

This paper has explored two novel metrics for evaluating the "strength of consciousness" within complex systems: one based on the sequential processes involved in consciousness, and another informed by Bayesian statistical approaches to assess the correctness of responses to observed events. The first metric, which focuses on the processes occurring at each step from sensory observation to post-hoc conscious awareness, provides a detailed examination of how quickly and effectively a system responds to stimuli. This approach highlights the temporal dynamics of consciousness, emphasizing the role of response time and information processing at each stage.

The second metric introduces a Bayesian framework to evaluate the accuracy of a system's responses over time. By incorporating the probability of correctness in decision-making, this model accounts for the iterative nature of learning and adaptation, where systems progressively refine their actions based on past outcomes. This method allows for a probabilistic assessment of consciousness, reflecting the evolving nature of decision-making and its impact on perceived consciousness.

Through the integration of these two approaches, we have proposed a unified model that combines the strengths of both process-oriented and correctness-based evaluations. This model not only assesses the real-time responsiveness of a system but also considers its ability to learn and adapt, providing a more comprehensive measure of consciousness strength. This integrated approach addresses some of the limitations of existing models, such as Integrated Information Theory (IIT), by incorporating both dynamic and probabilistic elements into the evaluation of consciousness.

In conclusion, the proposed model offers a robust framework for understanding and measuring consciousness across different systems. By uniting process-oriented metrics with Bayesian learning approaches, this model provides a holistic view of consciousness that captures both immediate responses and long-term adaptation. This work contributes to the ongoing development of consciousness theories, offering a testable and scalable approach that could be applied in both theoretical and practical contexts.

To ensure the reliability of the consciousness strength metrics proposed in this study, it is essential to conduct rigorous validation grounded in empirical phenomena, alongside theoretical evaluation supported by mathematical rigor. A careful and comprehensive assessment of the proposed framework's legitimacy must involve both empirical and formal lines of inquiry.