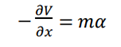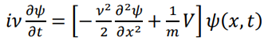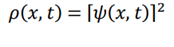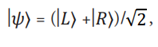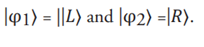Abstract
This paper discusses the interpretation of the measurement problem and Qbism in quantum mechanics using the Human Language based Consciousness (HLbC) model proposed by the author. The HLbC model holds that consciousness is generated from physical processes only. It adopts the position that consciousness is generated from physical processes only. Thus, for example, the choice between observing the behavior of electrons in a double-slit experiment as particles or as waves causing interference can be seen as purely physical processes in the brain. Qbism also considers the Schrodinger equation as a Bayesian probability for the mind, but it is known that the Schrodinger equation as an analogy appears in the process of consciousness generation in the HLbC model, which can support the Qbism position.
Keywords
Consciousness, Mathematical model, Human language, QBism, Quantum mechanics
Introduction
The measurement problem is an important issue in quantum mechanics that concerns how wave function collapse occurs. Various interpretations of quantum mechanics have been proposed because direct observation of the collapse of actual wave packets is not possible, and each interpretation raises significant questions. Examples include the double-slit experiment and Schrödinger's cat, for which different interpretations have been suggested. In particular, the relationship between quantum mechanics and consciousness is debated, and understanding how to incorporate consciousness into the measurement problem or whether consciousness is irrelevant to quantum mechanics is necessary [1]. QBism has been proposed as the ultimate idea in this regard [2]. While there exist excellent consciousness models such as the integrated information theory [3], there seems to be no consciousness model specialized in the measurement problem of quantum mechanics. The authors propose the HLbC model as a consciousness model and evaluate its validity [4,5]. As a result, the relationship between psychological consciousness and time was evaluated and found not to contradict existing knowledge. This paper interprets the so-called measurement problem in quantum mechanics using the HLbC model, which captures consciousness as a proposed physical monism. First, we describe several topics related to this paper.
Double slit problem
In quantum mechanics, the measurement problem refers to the question of how the collapse of the wave function occurs. The wave function is a mathematical representation that characterizes a physical system and is used to predict the probability distribution of physical quantities. However, it is not possible to directly observe the collapse of an actual wave packet, leading to various discussions about the interpretation of quantum mechanics. One of the most well-known problems in this regard is the double-slit experiment [6].
In the double-slit experiment, electrons are propelled from an electron gun through a plate bearing two apertures, ultimately imprinting upon a photographic plate on the opposing end. The resulting pattern, comprised of luminous and shadowed regions resulting from interference, akin to the undulating patterns cast by waves, offers tangible evidence of electrons' inherent wave-like behavior. Intriguingly, even as electrons are dispatched singularly, the resulting pattern remains consistent, hinting at an intrinsic wave-like essence associated with each electron.
However, upon meticulous observation of an electron's trajectory through one of the slits, the interference pattern on the photographic plate vanishes, replaced by a configuration resembling individual particle collisions. This transformation stands as compelling evidence of electrons' corpuscular nature.
Schrödinger's wave equation articulates electrons' wave-like behavior, intricately intertwining the wave function with state variables on a probabilistic basis. Yet, the apparent determinism in pinpointing an electron's position upon its collision with the photographic plate belies this probabilistic framework. Termed the "measurement problem" in quantum mechanics, the challenge of explaining this probabilistic "collapse of the wave function" remains a pivotal issue in interpreting quantum mechanics.
Despite its simplicity, the double-slit experiment poses a fundamental question in quantum mechanics: What is quantum mechanics? This paper delves into the double-slit experiment, interpreting it within the framework of consciousness, particularly within the HLbC model proposed by us. Additionally, we explore its connection to QBism.
QBism (Quantum Bayesian)
QBism regards probability as Bayesian probability and argues that there is no such thing as objective probability, and that each person has only subjective probability-beliefs about things they do not currently know. In other words, it is Bayesianism [2,7,8]. Furthermore, QBism adopts an individualistic interpretation of the quantum state as something that brings about the probability of measurement results (to the observer). That is to say, the allocation of quantum states represents not the physical state of the world, but the state of mind of the person observing it. The Schrödinger equation is not intended to determine the probability of the state of micro-particles, but rather to determine the subjective probability- beliefs of the observer as to what they will find when they measure it. According to this idea, all aspects of the structure and locality of spacetime in micro-particles, interactions with observation devices, and other characteristics can be ignored, and the subjective probability-beliefs of the observer for observation are all that matters. For example, to update personal "beliefs" about the results obtained through observation with high accuracy, and to improve one's own wave function, one only needs to increase the number of observations and repeat the learning process. It is claimed that the equation that represents this subjective probability is the Schrödinger equation. Since the result of observation is everything, and it is represented by the subjective probability, micro-particles and observation devices are irrelevant, and the "paradox" of the contraction of the wave packet is naturally resolved. Therefore, they also claim that Schrödinger's cat "paradox" is naturally resolved. In the conventional interpretation of quantum mechanics, since the wave function is the objective probability of micro-particles, it was necessary to consider subjective factors related to the observer and observation, such as interactions with devices and the convergence of wave packets. However, in QBism, the observer alone is the subject, and everything is determined by their subjective perspective, so there is no objective state until the observer sees. In other words, the act of observation itself determines the quantum state.
Brief Summary of the HLbC Model
The details of the HLbC model proposed by the authors have been described in detail in previous publications [4,5], so only a summary is given here. The concept of the HLbC model is shown in Figure 1. Consciousness generation by the HLbC model occurs in the following steps:
Figure 1. Concept of HLbC model.
[STEP-1]: Observation of events through the five senses.
[STEP -2&3]: Selection of a similar past episode from memory to the observed event. The episodes in memory may be composed of multiple events, each including emotions and actions taken in response to the event. Episodes stored in memory are composed of three elements: language or imagery, emotions, and the actions taken at the time. Each of these three elements is defined in a probability space, and episodes are represented as the Cartesian product of these three probability spaces. In the HLbC model, "similarity" is defined as a state where the Kullback-Leibler divergence between the observed event and the probability density function of memory is close. The selection of multiple similar episodes from memory is assumed to occur randomly due to pure physical noise, such as the state of the brain network or neurotransmitters. In other words, there is no free will in the response to observed events and reactions are determined entirely by noise within the brain. Based on the randomly selected memory, an actual action is taken in response to the event.
[STEP -4]: The result of the randomly selected action is stored in short-term memory.
[STEP -5]: The recognition process of "I did this action" by retrieving the memory stored in short-term memory is defined as "consciousness".
Since the STEP-1 - 4 can be purely explained by physical processes, the HLbC model is a consciousness model that follows physical monism.
Using the example of observing “a white dog running”, let's explain the process described above. STEP-1: This step involves observing "a white dog running" with your eyes. STEP-2: First, compare the observation result with the episodes stored in episodic memory. There may be multiple episodes, and episodes are expressed as [sentence] × [emotion] × [action]. For example, "a white dog running towards me" × "fear" × "escape" or "a white dog running towards me" × "adoration" × "play together," and so on. Even if the same words are included in the episode, the episode can have a different meaning depending on the emotion or action. Randomly select one of these multiple episodes and perform the behavior corresponding to the actual observation. In STEP-3, temporarily store the result of that behavior in short-term memory. In STEP-4, the moment of consciousness generation is defined as the point at which the result of the behavior stored in short-term memory is repeated. According to this interpretation, if someone is asked why they "ran away from a white dog running towards them," they will answer, "Because I had a scary experience being chased by a white dog when I was a child," and say that they acted based on their own consciousness. However, if they performed a behavior based on another episode, they should still answer that they acted based on their past episodes when randomly selecting their behavior."
Each process can be defined mathematically, but the details are omitted in this paper as they are described in detail in the paper by H. Hebishima et al. [4]. However, a summary of the selection of a similar past episode from memory to the observed event, which is necessary for the discussion in this paper, is summarized as follows:
This section delves into the intricate mathematical details of STEP-3: Modeling Decision-Making, as described previously. When we refer to "will," we are referring to our own volition. Essentially, if reality unfolds stochastically, the entity in question must embody this "will" towards the anticipated value within the probability framework. Initially, we center our focus on will as an expectation, and for modeling purposes, we define the "theoretical dynamics" of will. We conceptualize volition as the mechanism of altering the initial state probability framework to generate a new state probability framework. Initially, we define position x as the divergence between the probability space characterizing the initial state and the prospective probability space realized through will. While the Kullback-Leibler divergence serves this purpose, alternative metrics can also suffice. We posit that the Kullback-Leibler divergence serves as a gauge for the disparity between probability distributions, and its temporal transformation can be construed as a positional shift in typical dynamics. Furthermore, the temporal derivative of x corresponds to velocity and can be interpreted as the pace of alteration in the probability distribution, while the second temporal derivative can also signify acceleration α. Moreover, we contemplate, perhaps intuitively, the "inertia" of will. There exists a delay in recollection between the need to remember something and the subsequent action. We denote this degree of sluggishness as "inertia," and associate it with the decision-making mass m. The velocity and acceleration delineated above denote the processing swiftness post-recollection and are deemed as independent parameters of m. In this paper, we regard decision-making as a curation from historical behavioral data from episodic memory, and the aforementioned acceleration α and mass m should be intricately linked to past episodic memory. Analogous to dynamics, we then define the potential V of past episodic memory as a function to satisfy:
Let us suppose that m×α represents a force in classical dynamics, whereas within Eq. 5), we interpret it as a relation that defines the potential V, devoid of further connotations. It is logical to surmise that past episodic memory influences the velocity and acceleration of will and introduces potential as an indicative measure. All the aforementioned definitions of theoretical dynamics pertain to will as anticipation. Conversely, we contend that in actual decision-making, randomness is introduced by the state of the brain - encompassing neuronal states, among others.
As previously reported, when modeling STEP-2 as a random walk, an equation mathematically like the Schrödinger equation below is obtained [4,9]. However, it should be noted that this is an analogy, and does not mean that consciousness is governed by quantum mechanics.
Here, x represents the Kullback-Leibler divergence, t represents time, and ν is a parameter. ψ corresponds to the wave function in quantum mechanics and represents the probabilistic nature of decision-making, while the distribution function ρ(x,t) is connected when it settles into a state.
Comparison with Experimental Results
Let's consider the discussion of the experiment on the quantum aspects of consciousness conducted by J. Duffy and T. Loch-Temzelides [10]. They conducted a straightforward experiment. Initially, participants were asked to score their preference for green on a 10-point scale in response to the question "Do you like green?" (0 representing dislike and 10 representing like). In this case, responses generally fell into the categories of "2-3" or "7-8", indicating a nearly balanced distribution of preferences for or against green.
Next, participants were divided into two groups. For participant 1, contextual information regarding their initial responses was provided as a preamble, stating, "The score you selected is either '2-3' or '7-8' (see Figure 2)." Then, the question "Do you like green?" was repeated. This corresponds to the case of the double-slit experiment discussed in the previous chapter, analogous to awareness of the trajectory of a particle through a specific slit, akin to observing particle-like behavior in electron dynamics.
Figure 2: Concept of experiment of J. Duffy and T. Loch-Temzelides.
Conversely, for participant 2, information was presented with a preamble stating, "The score you selected is one of '2, 3, 7, 8'." They were then asked to reevaluate their response to the question "Do you like green?" This corresponds to the double-slit experiment in electron dynamics, where the trajectory of the electron through a specific slit remains undisclosed, akin to observing wave-like behavior. The outcomes of these scenarios are illustrated in Figure 3.
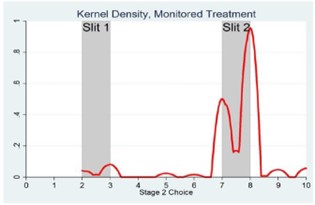
Figure 3: Quantum nature of will (cited from J. Duffy and T. Loch-Temzelides, 2021). a) Estimated kernel density, monitored treatment. b) Estimated kernel density, unmonitored treatment.
Duffy and Loch-Temzelides claim a significant difference in the distribution of choices in the second question (4). Specifically, they assert that participant 1's choices tend to exhibit particle-like tendencies, predominantly favoring the "2-3" or "7-8" ranges, while interference patterns were observed for participant 2. Based on this criterion, they conclude that volitional choices demonstrate quantum properties.
Interpreted as an indicative of quantum properties in decision-making, the aforementioned HLbC model appears to theoretically illustrate such interpretation. Regrettably, experiments concerning the quantum nature of decision-making are scarce. Future experiments are planned to rigorously scrutinize this matter further.
An Interpreting Measurement Problem in Quantum Mechanics
In the HLbC model, it is believed that when the human brain makes decisions, it searches for options from accumulated past episodic memories, and there is a probabilistic element involved in decision-making. In fact, if this process is modeled as a random walk, a mathematical equation like the Schrödinger equation is obtained. However, it is important to note that this is just an analogy and does not mean that consciousness is governed by quantum mechanics. In the HLbC model, choosing one option from countless choices is understood as one of the brain's functions. This process can be said to converge from countless options of wills to one, like the convergence of a wave function in quantum mechanics. However, in the HLbC model, the randomness of choosing actions is considered a fundamental concept of brain function, so there is no unnaturalness regarding convergence from multiple options. This selection process is guaranteed by the Axiom of Choice when considering episodic memory as a set that includes many elements. The Axiom of Choice is one of the fundamental axioms in set theory, asserting that for any given set, there exists a function f that can choose one element from every non-empty subset S. Symbolically, it can be expressed as ∀S ⊆ A (S ≠ ∅ → ∃x ∈ S), where ∀ is the universal quantifier (for all), ⊆ means subset, ∅ is the empty set, ∃ is the existential quantifier (there exists), and ∈ means belongs to. This means that for all subsets S, if S is not empty, then one element can be chosen from S. On the other hand, there is a difference between the material studied in quantum mechanics, which has wave-like properties, and the fact that the wave function spontaneously converges. In quantum mechanics, a measurement determines the state of the object being observed, and the observer's choice of what to measure is determined by the setting of the observation device, with the result being determined accordingly.
Quantum mechanics is a probabilistic theory, and the range of experimental conditions that humans can choose is limited. By selecting the experimental conditions, we can influence the behavior of particles, but we cannot fully control that influence. In other words, based on the uncertainty principle of quantum mechanics, by changing the experimental conditions, we can change the observed results of particles, but we cannot change the behavior of the particles themselves. However, although the behavior of particles is determined probabilistically based on physical laws, humans can influence the probability distribution by selecting experimental conditions. For example, in the double-slit experiment, interference occurs if the ratio of the slit width to the wavelength is within a certain range, but not outside that range. By changing the slit width or wavelength, humans can choose whether interference occurs within or outside that range. If the slit width is smaller than the wavelength, particles are expected to interfere as waves, whereas if the slit width is larger than the wavelength, particles are expected to behave as particles and no interference is expected to occur. By adjusting these conditions experimentally, humans can choose how particles behave. The important point is that which behavior is observed is determined by the experimental conditions.
When a physical system is projected onto a state by measurement, the state is transformed by the projection operator P. That is, if we denote the state before measurement as (ψ) and the state observed after measurement as |φ⟩, then (ψ) is projected onto |φ⟩ by the projection operator P. This can be expressed mathematically as |φ⟩ = |φ⟩ = |φ⟩ = |φ⟩=P|ψ). Here, P represents the projection operator, r,(ψ) represents the state before measurement, and |φ⟩ represents the state observed after measurement. The projection postulate is one of the axioms proposed to solve the measurement problem in quantum mechanics. It formalizes the concept of the projection of quantum states in physics and clarifies that a state is projected by measurement. This axiom explains the probability distribution of measurement results and the fact that quantum states change due to observation. It is explained by the following projection postulate.
If the slit width is smaller than the wavelength, electrons are represented as waves that interfere with each other.
Before observation, this state can be expressed as follows:(ψ)
where |L⟩ and |R⟩ represent the states of electrons coming out of the left and right slits, respectively, and √2 is a normalization constant. Using the projection operator, this state can be projected onto the following two states:
This choice is made by consciousness. However, the HLbC model argues that consciousness should be explained by physical monism. Therefore, the act of choice should also be seen as part of a physical process. However, if consciousness is considered a non-physical event, it becomes difficult to explain how the non-physical can influence physical phenomena such as particle behavior. In this sense, physical monism of consciousness is highly useful, as it avoids this problem. That is, we and the surrounding matter can be seen as an interdependent physical system in which physical phenomena and consciousness interact. We observe the behavior of particles through consciousness to understand it. On the other hand, in the HLbC model, consciousness itself is explained as a physical phenomenon, making it impossible to recognize objective particle behavior independently of the observer. This interpretation has also been adopted in the Copenhagen interpretation, but in this paper, it is believed that this problem is clearly explained by the HLbC model.
Next, let's consider QBism based on the HLbC model. QBism is an idea that puts all the foundations of quantum mechanics on the observer's (brain wave function), taking the probability that appears in quantum mechanics as Bayesian probability without considering the collapse of the wave packet, like the Copenhagen interpretation. On the other hand, the HLbC model states that the Schrödinger equation appears in the process of selecting the will in step 3 of consciousness, and since this is different for everyone, it can be considered equivalent to the brain wave function of the observer individual that QBism describes. Therefore, the HLbC model supports QBism. It is also conceivable that the Schrödinger equation, including the micro-particle being observed, the observing system, and even the interaction, synchronizes with the pseudo-Schrödinger equation that creates consciousness in the brain, both of which are possible interpretations.
In both QBism and the HLbC model, probability is treated in different ways. In QBism, probability is treated as Bayesian probability, and its cause is sought in the observer's wave function. On the other hand, in the HLbC model, it is stated that even if it is treated as normal probability, it is governed by the Schrödinger equation as an analogy for the process of creating consciousness in the brain. However, it should be noted that space x is the Kullback-Leibler distance.
Furthermore, the theoretical framework of QBism is developed based on the Schrödinger equation, but it can be directly applied to the Schrödinger equation as an analogy in the same way as the HLbC model. From this, it is suggested that if the HLbC model and QBism are equivalent, it is a very interesting result.
While the Copenhagen interpretation focuses on micro-particles and the observing system, QBism focuses on the observer. In the HLbC model, micro-particles and the observing system are regarded as consciousness, and it is also suggested that an analogous wave function is generated in the observer's brain. Since both interpretations lead to the same observational results, it is necessary to discuss the relativity of observation.
Thus, the HLbC model proposed by the authors reinforces the conventional standard interpretation of quantum mechanics and can be considered a valid one without contradiction. The HLbC model understands consciousness as a physical phenomenon, but it does not have elements to understand the behavior of micro-particles themselves.
The most important point of the proposed model is that consciousness is explained as a physical monism - i.e. the generation of consciousness is a purely physical process.
Conclusions
The HLbC model suggests that the human brain makes decisions by searching for options from accumulated past episodic memories, with a probabilistic element involved. This process can be modeled as a random walk, with a mathematical equation like the Schrödinger equation. However, this is just an analogy and does not mean that consciousness is governed by quantum mechanics. The randomness of choosing actions is considered a fundamental concept of brain function, and this selection process is guaranteed by the Axiom of Choice. The HLbC model and the QBism idea both consider the observer's brain wave function, with the former suggesting that the Schrödinger equation appears in the process of selecting the will in step 3 of consciousness, while the latter considers the probability in quantum mechanics as Bayesian probability without considering the collapse of the wave packet. The HLbC model supports QBism, which is based on the idea that the foundations of quantum mechanics are based on the observer's brain wave function. In both QBism and the HLbC model, probability is treated differently. QBism treats probability as Bayesian probability, while the HLbC model states that it is governed by the Schrödinger equation. Both interpretations lead to the same observational results, so it is necessary to discuss the relativity of observation.
References
2. Pienaar J. QBism and relational quantum mechanics compared. Foundations of Physics. 2021 Oct; 51(5):96.
3. Tononi G. An information integration theory of consciousness. BMC Neuroscience. 2004 Dec; 5:42.
4. Hebishima H, Arakaki M, Dozono C, Frolova H, Inage S. Mathematical definition of human language, and modeling of will and consciousness based on the human language. BioSystems. 2023 Mar 1; 225:104840.
5. Arakaki M, Dozono C, Frolova H, Hebishima H, Inage S. Modeling of will and consciousness based on the human language: Interpretation of qualia and psychological consciousness. Biosystems. 2023 May;227-228:104890.
6. Feynman RP, Leighton RB, Sands M, Hafner EM. The feynman lectures on physics; vol. III. Addison- Wesley, 1965.
7. Araujo M. Why QBism is completely empty?, 2019. https://mateusaraujo.info/2020/10/01/why-qbism-is-completely-empty/
8. Crease RP. QB or not QB? That is a question for quantum physicist and philosophers. 2019, https://physicsworld.com/a/qb-or-not-qb-that-is-the-question-for-quantum-physicists-and-philosophers/
9. Arakaki M, Hebishima H, Inage S. Interpretation and modelling of the brain and the split-brain using the HLbC (Human Language based Consciousness) model. Neurosci Chron. 2024;4(1):1-14.
10. Duffy J, Loch-Temzelides T. A double-slit experiment with human subjects. Plos One. 2021 Feb 11; 16(2):e0246526.